Turtle Time Trials & Leveraging Creativity To Deepen Mathematical Understanding

What if…?

In a lot of tasks that we give students, there’s an intended answer. Okay, sure, yes, I guess you could interpret the problem in this divergent way, but here’s what you should assume. This is what the writers of this problem meant. Here’s how you are supposed to engage.

Recently, our eighth graders reveled in a task where they were encouraged to experiment beyond those usual confines. Sure, this fits the situation we just experimented with, but what happens if you try something totally different? Something that turns the original scenario on its head? Let’s be creative with the mathematics! Let’s see what happens!

First, some context:

Turtle Time Trials

Turtle Time Trials is a gorgeously crafted lesson. (FYI it’s built into the Desmos 6-8 Math curriculum, but it’s also available as a standalone experience.) It gradually turns up the math dial, nudging a scenario from informal sensemaking to mathematical precision all within a 47 minute block. It is graceful. I scheduled myself to be in two different sections of eighth grade the day that we taught it.

The lesson launches with students watching a video of two turtles racing: one starts about halfway down the course, and moves slowly, while the second one starts at the beginning and moves at triple the pace. Students wrote stories to describe what’s happening.

• 

• 

• 

• 

• 

Some students used formal grammar conventions and punctuation, while others exercised creative liberties — “the blue turtle was secretly spiderman boom.” The classroom teacher shared a few examples. Not even five minutes into class, and we were already celebrating the plurality of voices. There were lots of ways to express what had happened, but the students collectively addressed the following major mathematical ideas:

• Rate or pace (and how one turtle moved faster)
• Position (one turtle had a “head start”)
• Directionality (this was implicitly addressed, as students described the scenario as a ‘race,’ from one point to another)

Increasing Mathematical Precision: Tables

On the next screen, we added a layer of mathematical precision: tables. To support their work with the table, students now had a timer tracking every tenth of a second, and a number line revealing the turtle’s position.

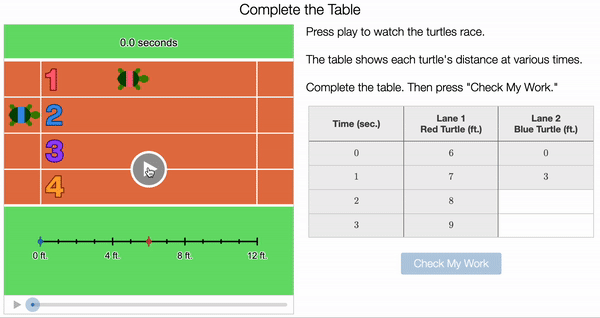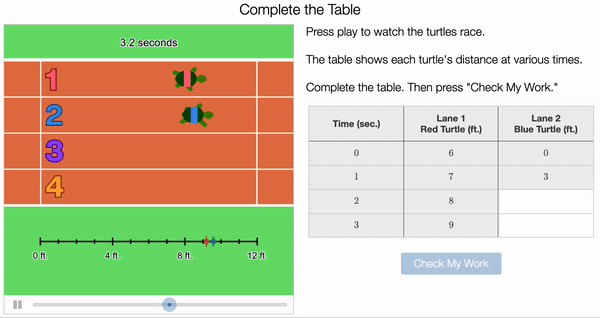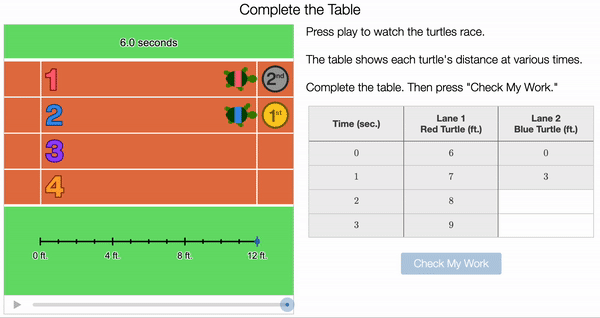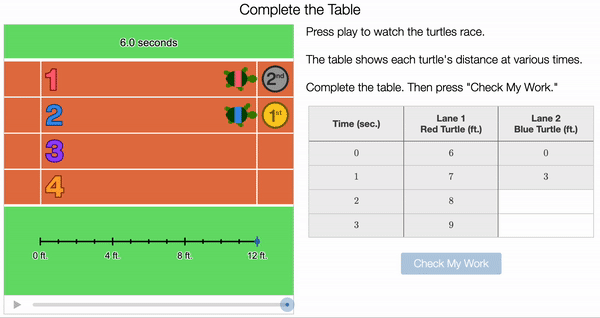
Students were then asked to calculate the speed of each turtle. Some students noticed that you could easily identify the rate for Turtle 2 (Blue Turtle). “It says 3 ft for 1 second, so it’s 3 feet per second. This is calling back all of the work we did in 6th and 7th grade around rates and proportional relationships. (There were even a few lessons on proportionality that involved turtle races.)

Adding Another Layer: Graphs

After some exploration of the tables, students add on another layer of mathematical precisions: graphs.

Students could see Turtle #1’s Head Start in the y-intercept of the red line. We asked students what the steepness of the line tells us, and what the point of intersection means. These are some big, heady conversations for the first lesson in the unit, but students came prepared. They’d built up considerable background knowledge about these racing turtles as they moved through mathematical representations.

Adding One More Layer: Equations

Finally, we finish our beautiful trifecta of middle school mathematical representations with equations.

Students experimented with different equations.

Entering yielded a turtle that raced neck and neck with Turtle #3 (purple).

Entering yielded a turtle that didn’t move at all! That variable serves an important role in our equation.

Entering sent the turtle flying. went even faster.

The turtle for moved at an almost imperceptible rate. “At this rate, how long will it take for the turtle to finish the 12 ft. race?”

And now…

I throughly enjoyed the discourse around the different mathematical representations for the turtle time trials, and also the best was yet to come: creating their own lines. Students were asked to draw lines to represent four new turtles, racing along the same 12 foot path.

Up until this point, students have experience with proportional relationships. It would make sense, then, that they would create lots of straight lines through the origin. And certainly some did!

But wait…

What’s this?

What is happening here?!

“Can You Make the Turtles Go Backward?”

“Ms. Laib, can you make the turtles go backward?” Rafa asked.

“Hmm. What would that graph look like?” I nudged.

Rafa drew a line elegantly sloping downwards, and hit ‘play.’ The turtle wiggled its way down the lane, a slow and steady moonwalk from right to left.

“Guys! Guys!” Other students’ ears perked up as Rafa’s excitement rippled through the classroom. It was like he had just discovered a curricular easter egg. “You can make the turtles go backwards!”

“How do you do that?!” Luis called from across the classroom. We’ve had issues with students in this class constantly calling to friends across the room, but this interruption felt productive. Contagious. Deliciously subversive.

Still, I interrupted to avoid a mathematical spoiler: “how do you think you would do it?”

Luis’ lip turned into a pout, and he returned to his computer to mess around with it. Other students seemed similarly motivated to experiment.

Maeve drew a series of straight lines, zig zagging back and forth across the quadrant.

“What do you think that will look like?” I asked her.

“I mean… I guess mountains?”

“Oh, I mean, let’s tell a story about the turtle based on your graph,” I clarified. “What will the turtle’s movements look like?”

“He moves forward and then back and then forward.”

Maeve hit play.

The turtle ambled forward, before quickly retreating into some sort of cosmic slingshot.

“He’s like a rocket!” Maeve exclaimed.

“Yes! What about your graph made the turtle go so fast?”

Maeve paused, and pointed to the third part of the piecewise function, with the steepest slope.

“Yeah, it’s almost vertical,” I said, using my arm to illustrate the meaning. “That’s a very, very steep slope. That turtle is moving at warp speed.”

“Are we allowed to make squiggles?”

Vanja drew this curvy masterpiece. He decided not to make horizontal or vertical lines — note the slight slant — but did dabble in this beautiful squiggle. What would it make the purple turtle do?

I watched this clip several times. The red turtle is barely visible, seeming to move faster than the speed of light. The movement of the blue turtle is imperceptible; it does not seem to advance over the course of the 12 second clip, and yet it ends slightly further than it started. The orange turtle walks at a consistent pace backwards. Meanwhile, the purple turtle stops and starts. It sputters. Briefly, it looks like multiple turtles appear, betraying the fact that what the student intended to be a function had some unintentional overlap.

I noticed that most of the questions students asked — “are we allowed…” “can you make…” — were asking for permission to experiment. Is it okay to go off book? Our answer was an empathetic yes. The visualization of the turtles offered instant feedback to students about their experiment.

The Class Discussion

These student created scenarios weren’t unlocking a mysterious Desmos easter egg. Instead, they were, in fact, the intended experience.

We intend for this to be a creative experience for students. We encourage you to emphasize those virtues whenever you see them in class.

Desmos Teachers Guide (Grade 8, Unit 3, Lesson 1)

With that in mind, the classroom teacher selected a few student generated graphs to share.

The Case of the Teleporting Turtle

We shared this one during the class discussion. “What will this look like? Why do you think that? Turn and talk.”

I listened to student conversations with the same manic energy a cartoon villain has right before explaining his scheme.

“He’ll go fast and slow and fast and slow and fast and slow.”

“The orange turtle will go fast and then pause and then super fast and then pause and then super fast and then pause.”

“The red turtle will go the fastest, and the blue turtle will be close behind, and the orange turtle… what is he doing? Smelling flowers? He doesn’t even finish the race!”

So: we showed the clip.

The students had understood a lot about the situation: the red turtle was the fastest. The orange turtle did pause, and never finished the race. However, the movement of those vertical lines was not something they had predicted.

“Is the turtle teleporting?!” Alvaro shouted out. The students laughed, and also it was a brilliant question.

“Yes, why does it look like the orange turtle is teleporting?!”

Silence

“I think because at 4 seconds…” Vanja started. “Okay, so it’s at 4 feet at like 3.99 seconds, and then all of a sudden it’s at 8 feet at like 4.01 seconds.”

“Yes, you’re paying close attention to what the axes mean in this graph. The measurement along the x-axis — the horizontal one — is time. Then the y-axis — the vertical one — shows us the distance. What does it mean that at 3.99 seconds the turtle is a distance of 4 feet, and at 4.01 seconds the turtle is a distance of 8 feet? And what would it really look like at 4 seconds if we could take a quick picture?”

Hmm, maybe I was losing them a little there. Maybe we could discern more about the nature of functions by looking at the next graph.

“Why is it so glitchy?”

The classroom teacher selected this one as our next graph.

“What about this one? What will the red turtle’s journey look like?”

The students were quieter. “Maybe there will be one turtle who stays the same, and one who goes super fast…?” one student theorized.

The students looked pained, as if they were staring directly into the sun.

“Wait… why is it so… glitchy?”

“It’s a monster!”

“Well, let’s see what’s going on with the graph!” The classroom teacher implored.

We watched the clip again, pointing to the motion of the dots on the graph. Then we watched again.

“Do you see why it might seem glitchy? Like there are two turtles?”

“…or three,” Rafa whispered.

“Say more about that.”

“You can see three dots,” Rafa continued.

We asked him to come to the board to show what he means, and he indicated the three dots that appear when there are three simultaneous outputs for 0.5 seconds.

Neither the classroom teacher nor I had spoken with the student that made this in advance, and my hunch is that they were trying to draw the lanes rather than draw a graph of the turtle’s journey. All the same, it was a great way to explore the nature of functions.

Return of the Straight Lines

This was the final work sample that we decided to show:

“What will this look like?”

The students predictions were more accurate for this one. Maybe it’s because they had more experience with straight lines over the course of the lesson, but I think that both their experiences playing around with this screen and our conversation about previous functions contributed to this knowledge.

Students noticed that the turtles will all end in the same place. “…but it’s not the end of the race?” They noticed that the turtles all seem to be moving at different speeds. There was some discussion about whether all of the turtles were moving forward.

“The graph looks nicer than the turtles,” Sofia mused. It was true: the lines on the graph came to a satisfying point at the end, whereas the turtles all moved at different rates and in some different directions. It looked chaotic.

“Are any of the turtles moving backwards?”

“Only the red… oh, it’s the only one with a negative slope,” Maeve said.

“The blue one takes 12 seconds to go one foot,” Vanja said.

“How can you tell?”

“At zero seconds, it’s at 8 feet, and then at 12 seconds, it is only at 9 feet.”

“I wonder if you could then use that to help you calculate a rate…” I started, but a quick glance at the clock told me that we were perilously close to the end of class. The classroom teacher shared the last snapshot collection of student work.

Synthesizing the Lesson

This was the first lesson in our eighth grade unit on linear relationships. Students had engaged with lots of important ideas, but, ultimately, we wanted to hit a few major ideas at the end of the lesson.

The classroom teacher selected responses from three students about using tables, graphs, and equations, and shared them with the class.

Ultimately, while these feel like three entirely different responses — how many feet, the slope, the coefficient — they’re all describing the same relationship. These are some of the biggest, meatiest ideas of eighth grade math.

Synthesizing the Experience

The arc of this lesson is something to behold: shifting seamlessly from tables, to graphs, to equations, and then giving students time to experiment with more creative graphic representations. The way that the Desmos activity makes the graph instantly visible as a context provides helpful feedback. Can we make the turtle go backwards? Let’s try this… hmm, that didn’t quite do it. Let’s try something else.

Sometimes, students were creative in ways that were less productive for our study of linear relationships.

These students creations weren’t totally useless, but, well…

Perhaps these student work samples aren’t serious enough for math class. Even if half of the students had drawn orange cyclops triangles, paying no attention to how this shapes the turtles’ movements, it still would have been worth it to me. The majority of the lesson was spent on strictly linear relationships, and giving students a little bit of freedom to explore other things yielded beautiful conversations in both of the eighth grade classes I witnessed.

Using divergent examples to anchor the classroom conversation, like the teleporting turtle and the glitchy race, communicates an important message to students: when we try different things, the math doesn’t break. Instead, we’re able to understand even more about the nature of these representations and the relationships they model.

When we’re creative, we can learn more.