In my last blog post, I described three ways in which Allison Hintz and Antony Smith’s Mathematizing Children’s Literature (Stenhouse, 2022) has disrupted how I think about the use of children’s literature in math class.
- Disruption #1: The book doesn’t need to be super mathy.
- Disruption #2: The book can and should be read multiple times, with multiple lenses.
- Disruption #3: Center student ideas and grow the experience together, rather than coming in with a pre-made plan.
I decided to try out some of the ideas from the book in a first grade classroom, using Two Many Birds, by Cindy Derby (MacMillan, 2020).
Selecting the Text
I first learned about the book from a webinar Kassia Wedekind gave for Bookelicious in March: “Math in Funny Places! Using Books that Make Us Laugh to Build Community and Meaning in Math Class.” My own children, ages 6 and 4, happened to be watching the webinar over my shoulder. “Mama! We have to get that one!”
And so I did. And we loved it.

In the book, birds queue up to perch on a tree, while an authoritative enforcer barks out rules at them: “
As birds line up to perch on a tree, a monitor shouts rules at them: “no running! No yelling! No fluffin’ the feathers!”

The rules get more and more absurd, and eventually the tree fills to capacity (100 birds). And that’s only the beginning. There are some twists and turns, and my children laughed uproariously at the enforcer’s fruitless attempts to control the situation. The book ends with some beautiful optimism about community, and some truly complex and nuanced messaging around rules and policing and sustainability. This is a book I could read 100 times and still wrestle with the ideas.
This book was not overtly mathematical — the math did not drive the story — but it was also ripe with mathematical possibility™. There’s the tree with a capacity of 100, the counter detailing how many birds are currently on the tree, the trees at the end of the story…
Planning for the First Read: Open Notice and Wonder
I first approached one of our first grade teachers, Addison, with the idea to mathematize this book. Her class would be a great fit for this experiment: Addison is passionate about children’s literature — she has the most enviable classroom library — and she always listens to student ideas with genuine curiosity. She kindly dedicated some time before school vacation week for the class to explore. I told her that this would involve multiple reads.
I committed to launching the investigation with an “Open Notice and Wonder.”
Using the Planning Template
I used the “Open Notice and Wonder Planning Template” (Appendix A) from Mathematizing Children’s Literature. It guided me to:
- Read and enjoy the story.
As a teacher and reader, what did I notice and wonder? - Anticipate and mark intended places for pausing the story.
What do I anticipate will be interesting or curious to my students?
(I put sticky notes to mark pages.) - Plan for story launch.
With my stopping points in mind, how will I introduce the story using the cover? - Gather chart paper and different-colored markers.

I didn’t record every single thing that I noticed and wondered in that top box, although it was helpful to jot down a few ideas and to continually ask myself to monitor my own thinking as I read the book again. (Even though my children weren’t there, I caught myself smiling about a few particularly funny pages.)
I couldn’t decide what to call the gray bird in the book: the enforcer? the officer? the lifeguard? I was curious about what the students might decide to name him.
This book does not have page numbers, so it was especially helpful to jot down notes about when to stop and then place sticky notes on the pages, something Hintz and Smith explicitly call out both in the book and on the planning form.
The mathematics that spoke to me the loudest was the record of the number of birds in the tree compared with the maximum capacity (100). If there is one bird in the tree, how many more birds from the line can join? If there are 13 birds in the tree, how many more can join? This connects nicely to our next unit explores the number system (TERC Investigations: Grade 1, Unit 7 – “How Many Tens? How Many Ones?”). However, students have not yet started the unit, so I wonder what math they might focus on?
Preparing Materials
I walked into the first grade class with the book, sticky notes popping out like mushrooms after a storm.
I decided to represent student thinking on a whiteboard. It might have been better to get chart paper, but, in the moment, I was going to work with what I had. I quickly pulled dry erase markers in several colors so that I could switch between pausing points.
We gathered students at the rug, and I introduced the book.
The Interactive Read Aloud!
“Today, we’re going to read a book called Two Many Birds. As we read, I want you to think about what you notice, and what you wonder. Be curious! Some of those things might be mathematical, and some of them might not. I really want you to enjoy the book. It’s funny!”

We looked at the cover. These birds were not like the sparrows and starlings we saw outside in our school’s bird sanctuary, which happens to be right outside this classroom. Look at the color! The vibrancy! Students were intrigued!
I recorded a few ideas in blue marker on the whiteboard. Students wanted to know what would make birds stand in a line. What do birds do that would possibly require tickets?
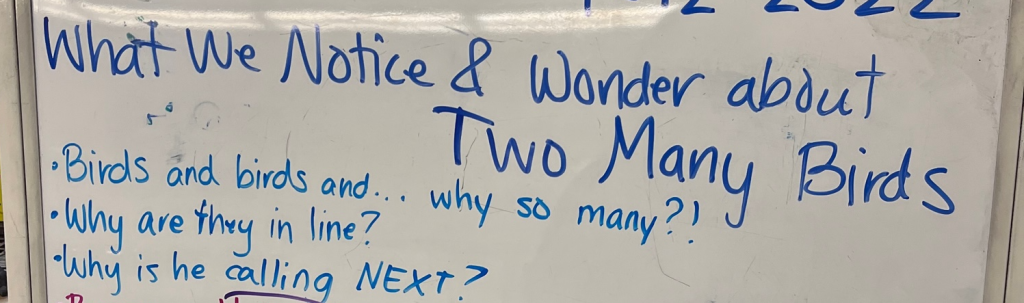
We continued to read. Students raised their hands throughout, although I mostly called out them on the pages I had planned as places to pause. If we stopped on every page, we’d lose the narrative drive of the story!
And then…
“Why are they all crowded on the tree, and why are their heads dots, and why is that owl being so bossy?”
Yes! We were only a few pages in, and the Enforcer already had a proposed name! Bossy Owl! (Later, I would ask the students again about this name, and other proposed “Chickenhead,” “Mr. Cheesyboo,” and, to my surprise, “Ms. Laib,” which made me question all of my choices leading up to that moment.)
We paused at the page with 13 birds.

Students were fascinated. Why is there a nest on that one bird? Does the nest count towards his hair? (The sign on the chair says “hair must NOT pass this line,” and the line seems to have been moved two times.) Will the bird make it onto the tree? Why is the bossy owl keeping track of how many birds are on the tree at all?

Then Leon pointed out something. “There’s 11 birds on there!”
I feel like that “record scratch” sound must have been audible. What?!
“Let me move the sticky note on the page,” I offered. It revealed a hidden bird, and Leon looked visibly disappointed, but wait… he was onto something.

Well, well, well.
“Someone’s getting on!” a student called out excitedly.
I recorded it on our chart of things we notice and wonder.
Saoirse waved her hand frantically. “That was true on the other pages, too!”
“Say more about that!”
“On the page that said 2, there was only one bird on the tree!”

Well!
I couldn’t help myself from following their pattern. “And what about on the page where the tracker said “1”?
“ZERO!” Students called out in chorus.
“And what if the tracker had read 17?”
“SIXTEEN!”
“Or 30?”
“TWENTY-NINE!” students chanted, albeit with stumbles and different starts, which made all of the “nines” echo throughout the classroom like we were in a bat cave.
“Okay, sorry, I couldn’t help myself,” I offered, only half-apologetically. “There’s so many cool math ideas in this book. But let’s keep reading! I can’t wait for you to see what happens next.”
We continued to read. I hadn’t planned to stop here, but students could barely contain their glee at this page.

The students really fixated on not just how ridiculous the rules are — “no blinking? birds have to blink! Everything has to blink!” — but also the hypocrisy of the Bossy Owl resting and pesting when doing exactly those things. It’s first grade: the most important thing in the world is that things are fair.
And students continued to laugh! How often do we get to hear genuine peals of laughter while reading a book in math class? (I do reign in the chaos towards the end of that audio clip, but we burst into laughter again a few pages later.)
I continued to pause — mostly at the intended stopping points — and record some student thinking. As time went on, we talked more and recorded less. There simply wasn’t enough space.

At the end of the book, I informed students that we would read it again the following day, and dig deeper into some of their mathematical noticings and wonderings. The students burst into applause. I was Sully landing the plane on the Hudson. It was an odd feeling for math class, but the joy was palpable.
Planning for Tomorrow
As the students ate their snack, I gathered with the classroom teacher in the back of the room. We reviewed the student ideas I had recorded, and mentioned some of the ideas that I hadn’t.
“You forgot to record the part where the kid said that if there is one on the tree, there’s room for 99 more,” she pointed out.
“Oh, right! That wasn’t at one of our pages to pause on, and it got kind of lost in the shuffle,” I confessed. Instead, we had spent longer talking about how the number on the tracker was always the number of birds in the tree plus one bird entering the tree (n+1).
“I think that’s the big idea we want to use,” she nudged.
“Yeah, I think there’s a lot of potential there. I think we could also use it as a formative assessment as we enter into the next unit, How Many Tens/Ones.”
We then considered what students might investigate, e.g. if there are 13 birds on the tree, how many more from the line can join? We also considered what mathematical tools students might be familiar with, and what might be helpful. Should we make ten frames available as they are working? Should we have hundreds grids available? Should we give them lots of blank space? How much of the book should we re-read in order to activate the thinking?
We started to work on Appendix C from Mathematizing Children’s Literature: Focused Read Planning Template.
Disrupting How I Teach with Children’s Literature in Math Class
Here are the three disruptions that I named earlier in the blog post:
- Disruption #1: The book doesn’t need to be super mathy.
- Disruption #2: The book can and should be read multiple times, with multiple lenses.
- Disruption #3: Center student ideas and grow the experience together, rather than coming in with a pre-made plan.
The classroom teacher and I were pleased with just how many mathematical ideas surfaced from this book that wasn’t “super mathy.” The first reading had been liberating: we were able to talk about a lot of the story, and hear from students. It is only because we had planned time for a subsequent reading — or maybe more? — that we felt like we could give ourselves space to understand and enjoy the book, and build community.
Because I did not have one mathematical exploration definitively planned out before starting the lesson, we listened to student ideas with greater curiosity. We shaped subsequent learning experiences from student ideas, in collaboration with the entire class.
Students exercised a sense of agency. They are the sensemakers, and they are capable of recognizing mathematics in all different contexts.
There will be more about that in tomorrow’s blog post — part two!


Reserving this one from the library — it looks like a lot of fun!
LikeLiked by 2 people