This game is part of my “simple but high leverage” collection of games that are flexible, engaging, and easy to prep. Others include The Answer Is… and the Skip Count Game.
I have always assumed everyone else played this game. I held this assumption even when I did not have a name for this game. (What do all of you call this game?) I let students vote: “Mystery Boxes,” “Open Middle,” and “Multiple Choice” were all student suggestions.
I think I’ve settled on “Number Boxes” For now. Please let me know if you have a better name.
This Game, In a Nutshell:
This game involves writing down numbers (randomly generated by a die, spinner, cards, etc.) on a recording sheet. Once the number has been placed, it cannot be moved. Two numbers on any given round may be “thrown away.” Play continues until all of the boxes are full. Students are working towards a specific target.

Some people think of this as a place value game — students put digits down, unable to move a digit once its placed, attempting to make the largest number. I think this game is far more flexible than that. This game is the ultimate chameleon! I’ve used it with 6 year olds and 16 year olds. It transforms itself to fit different content, different learning goals, and different mediums. I’ve played it using pencil on paper, dry erase markers on windows, and using desmos.
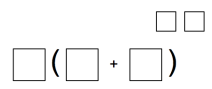
Because I think reading an example of the game in action may be more helpful than reading the directions, here’s an example. (Directions also available here)
A Sample Round with Fourth Graders Exploring Multiplication
I drew the following six boxes on the board.
Then I asked students about they noticed and wondered.
“There are six boxes”
“It looks like a multiplication problem.”
“Why are two of the boxes small and in the corner?”
Then I asked students to create their identical board on a whiteboard, but I could have given them physical copies of pre-made boards, or had them write on paper, etc. This is creating a recording sheet.
Then I pulled out a simple six sided die to generate random numbers.
“I’m going to roll the number cube,” I told the students. “When I say the number, you can write it down in any of your six boxes. Here’s the important part: once you write a number down, you cannot change its placement. It’s stuck.”
Students nodded, so I continued.
“The two small boxes in the corner are your ‘throwaway boxes.’ You are able to ‘throw away’ two numbers over the course of the game that you don’t want to use. Choose wisely! Once you write a number in a throwaway box, it’s there permanently.”
Then I announced the target. “Here’s the most important thing: your goal is to get the largest product you can.”
 *I have considered changing the term “throwaway box” to something more ecofriendly, “recycle box,” but that didn’t seem to fit as well. The numbers can’t be reused.
*I have considered changing the term “throwaway box” to something more ecofriendly, “recycle box,” but that didn’t seem to fit as well. The numbers can’t be reused.
I rolled the following numbers: 3, 5, 1, 6, 2, 1
Many students decided to throw away the smallest numbers, leaving them with the largest. However, this lead many of them to toss the 2, not realizing that the final number rolled would be a 1.
-
53 x 61, throw away 1 & 2
-
32 x 56, throw away 1 & 1
-
51 x 63, throw away 1 & 2
Which of these products it the largest? Students were able to use multiple strategies — including partial products, open arrays, and the traditional algorithm. Students theorized that 53 x 61 and 51 x 63 might be equal, because the ones digit is just changed, but it turns out it made a more sizable difference in the final product. But why?
“61 and 63 are really close together, but in one problem you have 53 groups of it and in the other one you have 51 groups. Fifty-three groups is bigger.”
We decided to play again, but I changed the target. The second time, I wanted students to aim for a product that is as close to 1,000 as possible. Students eyes widened. They needed to develop some new strategies for where to place the numbers, and which ones to throw away.
Why I love this game:
- It’s accessible. It’s more fun when students are able to develop strategies about where to place numbers, but anyone that is currently learning about the selected content can play for practice even if the numbers get placed randomly.
- It helps students look for and make use of structure (SMP7).
- It requires few materials. Thankfully, all of these materials can be spontaneously gathered. Nothing needs to be copied in advance. With about 30 seconds notice, your class can play this game.
Choosing the Content
First, choose a topic: are your first graders working on addition? …your fourth graders working on multiplication? …your eighth graders working on systems of equations?
Primary Grade Content

Adding within 100
Potential Targets: largest sum, smallest sum, closest to 20, closest to 40, etc.


Multi-digit addition
Potential Targets: largest sum, smallest sum, closest to 100, furthest away from 50, etc.

Addition and subtraction with two-digit numbers
Potential Targets: largest final amount, closest to 0, closest to 30, answer that goes below zero (without asking students to calculate the final amount, etc.
Upper Elementary Content

Place Value
Potential Targets: largest number, smallest number, closest to 4,000, etc.

Multi-digit Multiplication
Potential Targets: largest product, smallest product, closest to 1000, closest to 2400, etc.
Middle School Content

Exponents
Potential Targets: largest sum, smallest sum, closest to 50, etc.

Expressions/Distributive Property
Potential Targets: Closest to 20, closest to 40, an odd number over 35, etc.
Number Boxes
directions available for download
Grade level: any grade where students can write numbers and perform operations
Time Frame: at least 5 minutes, ideally more like 15, and conceivably 30+
Materials:
- Something to create a recording sheet. (e.g. paper, whiteboard, an accessible window that students will write all over using dry erase markers, etc.)
- Something to record on the recording sheet (e.g. pencil, marker, etc.)
- Something to generate numbers (e.g. dice, spinner, cards, random generator app, little slips of paper with numbers on them, etc.)
Planning:
- Design a learning goal. Maybe your learning goal is related to a current topic of study, or maybe it’s review.
- Design a recording sheet. See content examples above.
Procedure:
- Students write (or receive) the recording sheet.
- Teacher announces the target.
- A facilitator (teacher or fellow student) rolls a dice/spins a spinner/etc., and calls out the randomly generated numbers
- Students record the numbers on their recording sheet. Once a number has been place, it may not be moved. Students are all recording the same numbers. If the facilitator calls out 3, all students must place it on the board.
- The game ends when all of the boxes are full.
 Playing Number Boxes on a window, with a target of “greatest product”
Playing Number Boxes on a window, with a target of “greatest product”


Truly a flexible game! I’ve always called it “Place Value Game” because where you place the number affects the final value, but I like your name “Number Boxes” better.
LikeLiked by 1 person
I think I learned it as the Place Value Game, too! It’s great with any name. 🙂
LikeLike
I play this game in math all the time in my 4th grade math class. It is so adaptable. We use it for multiplication, division, subtraction, addition, and this year I tried it with adding or subtracting fractions with the same denominator. We call it Beanpot and students love it!
LikeLiked by 1 person
I like the name Beanpot!
It is such a great game for fourth grade. 🙂 (That’s where I first played it, back when I was a classroom teacher.)
How did it go with adding and subtracting like denominators? I’d love to hear more about how you set it up & student thinking.
LikeLike
Trash can math. The throwaways are Trash cans
LikeLike
Just stumbled across your twitter post. Love this. My middle school math support students have not responded well to the open-middle type problems. My feeling is that they need to develop some stamina for productive struggle and, besides being a great activity in its own right, it offers scaffolding to build up to open-middle activities.
LikeLiked by 1 person
Hello,
I played your game today making the greatest number. We liked it. We are first graders. We used two throwaway boxes and two boxes below. We rolled 4 times and each roll we placed a number in a box. We were trying to make the greatest number. The game said that if you put a number in a throwaway box, it’s there permanently. For each new round, students can erase all numbers correct? Thank you for such a fun game.
LikeLiked by 1 person
I’m glad the first graders had fun!
And, yes, students can erase all of the numbers in order to start a new round. 😀
LikeLike
I really like this game and will use it this upcoming year in the 6th grade. I do have one question. As you are reading out the numbers, can students move the numbers around the boxes that are not the “throwaway boxes”?
LikeLike
I typically play with the rule that students cannot move a number after it has been placed. (And the number must be placed before the next number is announced.) You could always try it the other way, as long as you’re clear with the students! You may end up with a lot of ties. 🙂
LikeLike