Fourth grade teacher Alicia and I have a beautiful habit of doing math together when planning. We try out problems, and anticipate ways we think students.*
*This work is made possible because our schedules work out such that we plan together multiple times per week, and we don’t do it for every lesson, but still…
This practice has improved our ability to focus class discussions. For example, on Thursday, students in Alicia’s 4th grade had worked on prompts involving equal groups of a fractional amount (pizzas, measurements of cloth, etc.). Just as we had anticipated, some students had thought of this as repeated addition, and some as multiplication. We knew to monitor for this to select student work for sharing. Students then compared and contrasted the two ideas. We looked for connections. (This is in line with the 5 Practices for Orchestrating Discussion.)
So we pulled this task for the following day. It comes from Howard County (Maryland)’s bank of formative assessment questions.
Problem from Howard County (Maryland) Math Department, available here. See other tasks for standard 4.NF.4.
Alicia and I thought this fit perfectly.
“After today, I don’t think many kids will pick the first option,” Alicia mused.
“I like that the third option decomposes those groups of 3/4, and shows how they’re built from that unit fraction,” I added. “I haven’t seen anyone doing it like that, but I wonder if it will help a few students, like Harlow and Lukas, clarify their thinking.”
“I can’t think of anyone that would see this as subtraction,” Alicia continued. I agreed. “It wouldn’t match any of the models we’re talking about.
…which is why we were so surprised when a few students checked that off the following day.
Demitri’s work
Alicia and I did our best to interpret the work from paper.
“Oh, I think he was solving each problem instead of using reasoning,” I said. Alicia nodded in agreement. Demitri is a student who takes a rigorous math class outside of school, and so he often feels very ‘well taught.’ I continued: “and these numbers just happened to work out.” Ugh. Usually we check for things like that!
…but then we remembered Luna’s work from the previous day.
Luna’s Work
question from TERC’s Investigations 3 (Grade 4, Unit 6)
@Inv3_Math
The pizza task, despite having a different context, involved most of the same numbers: 3 groups of 3/4. Some students had written the answer as 9/4, and others as 2 1/4, but all of the answers were equivalent.
Luna’s work was different. (We considered sharing it with the class that day, but it didn’t quite get at the mathematical heart of the lesson: connecting repeated addition and multiplication equations.) Although her model had looked the same as everyone else’s — three round pizza circles, cut into quarters with horizontal and vertical lines, her equation showed different thinking.
This equation represents the three pizzas individually, as 4/4 each. Cumulatively, this is worth 12/4, or 3 whole pizzas. Then, she subtracted 3/4.
“For the three slices that weren’t eaten,” Luna had explained.
There it was.
Huh! It wasn’t a coincidence that these numbers worked. Alicia and I were surprised, and decided we had to share our new learning with the class.
“You know, Ms. López and I had done this problem together yesterday, and we thought we knew all of the answers. We selected options 2, 3, and 4,” I started, referencing my work with Alicia. We quickly discussed why these answers matched the cookie recipe context.
“But then we saw several of you had chosen the last one. 3 – 3/4.”
“But it’s not a subtraction problem,” I heard one boy whisper from the side.
“This reminded us of Luna’s work from yesterday.”
We showed Luna’s work using the document camera.
Luna helped us annotate her work. She also realized a small error in her equation — she meant to write 12/4 instead of one of the 3/4 in her original work — and wanted us to change it. It was easy enough with a dry erase marker.
Some students seemed as surprised as we did that the subtraction equation also matched the cookie recipe story!
“Will this always work with multiplication and subtraction?” Jason wondered allowed.
We returned to the cookie problem, to have students help us prove that the subtraction equation matches using a visual representation.
The real takeaway here is that, no matter how thoughtfully and deliberately Alicia and I anticipate student thinking, there will be some student work that can surprise us.
Upon reflection, I think the key factors here may be:
- Experience with avenues for thinking about the problem
I’ve built up my pedagogical content knowledge over time, seeing how students solve particular problems. Every time I engage with content, a student helps me add to my content knowledge, mapping out yet another way to think about the idea. Teachers who are newer to the field or newer to the course may not be able to lean on the experience of having observed students. This makes it even more important to develop the habit of doing math and anticipating student thinking — even if it’s not every day. It needs to be a sustainable practice. Alicia and I have found it helpful to have a buddy to engage in the work. - Listening to students
Probe their thinking, and listen to their explanations. Notice nuances in student work that represent differences in thinking. This serves may purposes: honoring the idea more precisely, honoring the mathematical work that went into generating this idea, honoring the student as mathematician… - Being open to changing or revising thinking.
Alicia and I know we aren’t the only math authorities in the room. We learn things from these fourth graders all the time. (We’re also open to making mistakes in front of the students, which didn’t factor into this particular story.) - Making connections
Luna’s work on the pizza problem connected beautifully to the work on the cookie recipe problem. We had to make the connection, though, and we had to help students make the connection, too. Students who see connections between mathematical ideas, representations, and concepts, develop stronger neural pathways — better learning. - Connecting visual representations
Students at the end were able to help us construct a visual that showed how the subtraction equation (3 – 3/4) could also match the situation of 3 x 3/4. This helped all of us — the students, Alicia, and me — deepen our understanding of the mathematics at play.
______
This particular pattern, that you can replace the multiplication operation with subtraction — 3 • 3/4 = 3 – 3/4 — works in some cases, but not all.
This will work with 4 groups of 4/5.
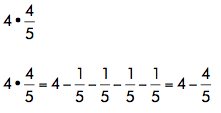
This will work with 9 groups of 9/10.
This will even work with 132 groups of 132/133.
In fact, it will work for any problem set up like this:
Because you can make x groups of 1, and then take away 1/(x+1) repeatedly, x times.
But this format wouldn’t work for any other relationship. For example,
…and we never would have stumbled into this pattern if it weren’t for Luna’s work and thinking surprising us, and going beyond what we had anticipated, the day before.
Embrace the Challenge 